Using black-box fuzzing is like firing a machine gun while blindfolded.
White-box fuzzing is like using a sniper rifle. Each shot is slow but, but it hits a new path every time.
Let me first show you a snippet of the results. We applied our lightgrey-box fuzzing named PathFinder to a well-known deep learning library, PyTorch. These plots show how branch coverage increases over time. Clearly, our approach overwhelmingly outperforms the existing SOTA tools using various approaches.
Moreover, as the exploration proceeds, the path conditions can become more precise since more data points for synthesis are available.
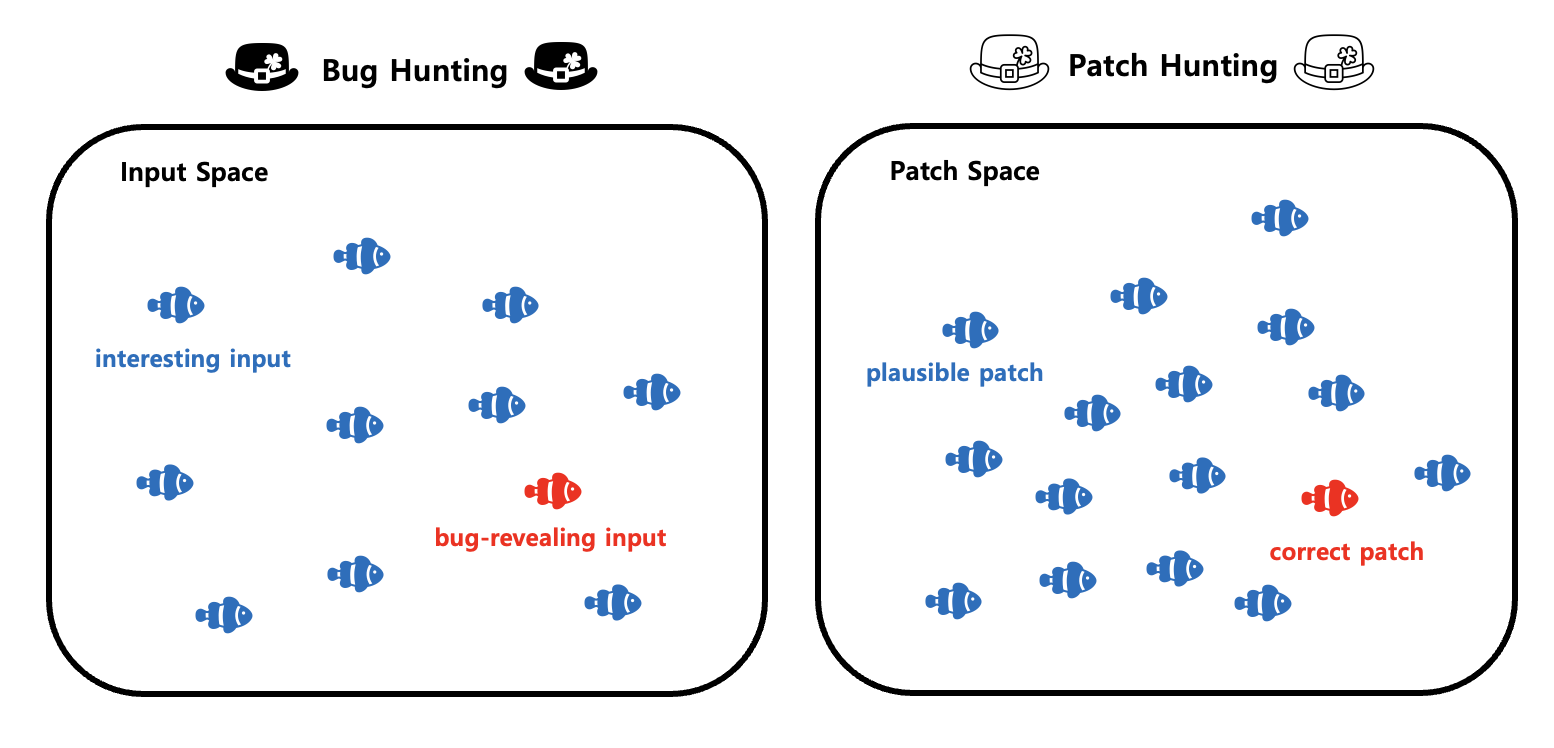
# Bug Hunting and Patch Hunting
---
Our situation can be specifically modeled as a Bernoulli bandit problem. We need to speculate the probability of success of each arm. And each arm can have a different probability of success.
The Bernoulli bandit problem can be solved by the Thompson sampling algorithm that works in the following three steps. First, for each arm $k$, we sample $\theta_k$ from its distribution. Let's say we are about to choose between method 1 and method 2. Let's assume that the left arm is associated with this Beta distribution and the right arm is associated with that Beta distribution. It is likely that a higher value is sample from the right arm, in which case we choose the right arm. However, note that Thompson sampling still allows to choose the left arm with a smaller probability.
- Distribution of $\theta_k$: Beta distribution $(\alpha_k, \beta_k)$
| $Beta(\alpha=2,\beta=2)$ | $Beta(\alpha=3,\beta=2)$ | $Beta(\alpha=5,\beta=2)$ |
| --- | --- | --- |
|  |  |  |
What if we find an interesting patch? Then, we update the distributions of the corresponding edges. For example, if this was the distribution of this edge before the update, its right-hand side one shows the distribution after the update. Notice that the distribution after the update is more left skewed, indicating that selecting this edge looks more promising than before.
Then the natural question that arises is: Can we invent a grey-box approach that performs better than the black-box approach?
---
# Blackbox Guidance Policy
- While traversing the patch-space tree, this policy gives higher priority to edges that are more likely to lead to the discovery of interesting patches.
- Note that the only runtime information used in this policy is whether a test passes or fails after applying a patch.
Each edge is associated with critical branches. These critical branches are obtained after executing interesting patches observed in the corresponding subtree. Unlike in the black-box approach, we assign a beta distribution to each critical branch.